遍历：DFS/回溯

问题一（统计个数）：下属个数

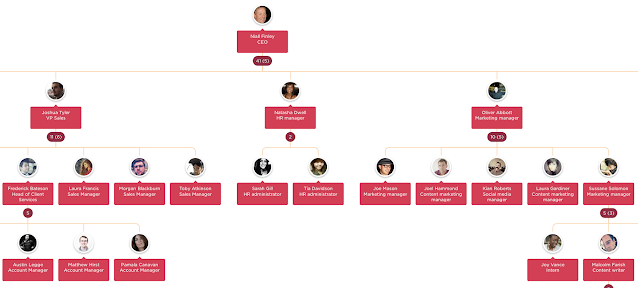
在一家公司中，我们需要知道每个员工有几个下属。那么我们给每一个员工一个分数Score：如果TA没有下级，那么Score=1，否则Score=下级的个数+1（自身）。我们把每一个员工看成一个节点，那么这个公司从CEO开始作为根节点就可以看作是一棵树。

那么问题来了：给定一个公司结构和员工号，我们如何查找TA的score？这样的问题一般用DFS来递归解决。

def dfs(graph, id):
    if id not in graph: return 0 # base case
    score = 1                    # 自己
    for e in graph[id]:          # 下属
        score += dfs(graph, e)
    return score

cache = {} # id: score
def dfs(graph, id):
    if id not in graph: return 0 # base case
    
    if id in cache: return cache[id]
    score = 1                    # 自己
    for e in graph[id]:          # 下属
        score += dfs(graph, e)

    cache[id] = score
    return res

DFS搜索经常出现的问题就是重复查询。比如说在这个问题中，我们两次分别查询员工与TA的老板，那么员工的score就是可以重复利用的信息。对于这样的重复子问题，有两种解决方案：

备忘录：在自顶向下递归的最外面加一个cache（或者memo）来存储已经求解了的答案。在动态规划的介绍中我们再重温这个话题。
动态规划：利用子问题的结构，用自底向上的方法来消灭重复查询。比如练习《验证平衡二叉树》，不像动态规划，然而用了这样的思路。

讨论：如果面对多次查找的同时，对树的结构还可能有改变（公司变动）。那么我们需要灵活改变cache(cache invalidation)来应对。比如我们可以拓展cache来存储以下内容cache: id -> score, manager_id, set(report_id)

这样一来，我们相当于拥有了对父节点（老板）的指针。一旦有一个subtree（部门）有改变，我们就可以向上遍历，来改动他们在cache中的score。

问题二（求解）：迷宫出口

给定一张迷宫，入口entrance与出口exit，如何从entrance到达exit？有两个方便的函数来我们进行选择和判断：

neighbors(p)来访问从p出发相邻的点
wall(p,q)来判断每个两点p与q之间是否隔着一堵墙

从起点出发进行搜索，而且我们的在每一个点的策略是，每次遇到选择就选择第一个可行解（neighbors(p)当中给我们的第一个结果，可以是向左转前进一格）。直到我们没有选择了再回头。如果有解（exit可到达），那么至少有一条路径是连接出入口的，我们把它记下来。

注意这里“第一个可行解“可能会排除以下选择：

已经走过的路：一般用path（走过的路径）或者vis（额外的标记数组）来标记
走不通的路：越界、隔着墙等不符合最后答案的选择。

这道题里neighbors(p)帮我们做选择，wall(p,q)帮我们排除不合法选择。

def dfs(path, p):
    if p==exit:
        res.append(path)
        return
    for q in neighbors(s):
        if q in path: continue  # visited
        if wall(p, q): continue # it's a wall
        path.append(q)          # 探索
        dfs(path, q)
        path.pop()              # 回溯

res = []
dfs([enter], enter)
return res

def dfs(path, p):
    if p==exit:
        res.append(path)
        return
    for q in neighbors(s):
        if q in path: continue  # visited
        if wall(p, q): continue # it's a wall
        dfs(path+[q], q)        # 新的path object!

res = []
dfs([enter], enter)
return res

在Python中有一个偷懒的解法。在上面非回溯解法中，我们+(__iadd__operator)来创造一个新的list。新的list（也需要新的空间）会来替我们搜索，就不需要回溯了。

可行解与所有解：有的时候我们不需要找到所有可行解，而是只需找到任意可行解。那么我们早早的就可以退出递归函数。

def dfs(path, p):
    if p==exit:
        res[:] = path
        return True
    for q in neighbors(s):
        if q in path: continue  # visited
        if wall(p, q): continue # it's a wall
        path.append(q)          # 探索
        if dfs(path, q):
            return True         # 找到可行解！
        path.pop()              # 回溯
    return False                # 没有可行解

res = []
dfs([enter], enter)
return res

验证平衡二叉树

“一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。“

这是一道简单题，然而有两种复杂度截然不同的解法。参考代码:

def isBalanced(root):
    def height(root):
        if not root: return 0
        left = height(root.left)
        right = height(root.right)
        if left==-1 or right==-1 or \
           abs(left-right) > 1:
            return -1
        return max(left, right) + 1

    return height(root) != -1

def isBalanced(root):
    def depth(root):
        if not root: return 0
        left = depth(root.left)
        right = depth(root.right)
        return max(left, right) + 1

    if not root:
        return True
    if abs(depth(root.left)-depth(root.right))>1:
        return False
    return self.isBalanced(root.left) and \
        self.isBalanced(root.right)

子集/排列

子集（Subsets）： $2^N$ 个幂集
子集 II（SubsetsUnique）：去重的幂集
全排列（Permute）: $n!$ 个排列
全排列 II（PermuteUnique）：去重的全排列
组合（Combine）： $\frac{n!}{k!(n-k)!}$ 个顺序无关的放球问题
组合总和（CombineSum）：每个元素可以取无限次，记得剪枝。方案数可以用完全背包DP解决。
组合总和II（CombineSumUnique）：每个元素最多可以取1次，枚举 $2^N$ 个子集记得剪枝。方案数可以用0-1背包DP解决。

输入：nums = [1,2,3]
输出：
[[],
[1],
[2],
[1,2],
[3],
[1,3],
[2,3],
[1,2,3]]

# iteration with state
n = len(nums)
res = []
for i in range(1<<n):
    res.append([nums[j] for j in range(n) if (i>>j)&1])
return res

# recursion
def dfs(path, i):
    res.append(path)
    for j in range(i, len(nums)):
        dfs(path+[nums[j]], j+1)

res = []
dfs([], 0)
return res

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

def dfs(path, i):
    res.append(path)
    for j in range(i, len(nums)):
        if j>i and nums[j]==nums[j-1]: continue
        dfs(path+[nums[j]], j+1)

nums.sort()
res = []
dfs([], 0)
return res

输入：nums = [1,2,3]
输出：
[[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]]

# recursion with state
def dfs(s, path):
    if s==((1<<n)-1):
        res.append(path)
        return
    for i in range(n):
        if not (s>>i) & 1:
            dfs(s|(1<<i), path+[nums[i]])

n = len(nums)
res = []
dfs(0, [])
return res

# recursion
def permute(self, nums: List[int]) -> List[List[int]]:
    def dfs(path):
        if len(path)==n:
            res.append(path[:])
            return
        for i in range(n):
            if nums[i] in path:
                continue
            dfs(path+[nums[i]])
    
    n = len(nums)
    res = []
    dfs([])
    return res

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

# recursion with state
def dfs(s, path):
    if s==((1<<n)-1):
        res.append(path[:])
        return
    for i in range(n):
        if s & (1<<i): continue
        if i>0 and nums[i]==nums[i-1] and not s&(1<<(i-1)):
            continue
        dfs(s | (1<<i), path+[nums[i]])

nums.sort()
n = len(nums)
res = []
dfs(0, [])
return res


# 切片法
def dfs(s, path):
    if not s:
        res.append(path)
        return
    seen = 0
    for i, c in enumerate(s):
        if not seen>>(ord(c)-ord('a')) & 1:
            seen |= (1<<(ord(c)-ord('a')))
            dfs(s[:i]+s[i+1:], path+c)
res = []
dfs(s, "")
return res

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

def dfs(path, i):
    if len(path)==k:
        res.append(path)
        return
    for j in range(i, n):
        dfs(path+[j+1], j+1)

res = []
dfs([], 0)
return res

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
  [7],
  [2,2,3]
]

def dfs(num, i, path):
    if num==0:
        res.append(path)
        return
    for j in range(i, len(candidates)):
        n = candidates[j]
        if num-n<0: continue
        dfs(num-n, j, path+[n])

res = []
dfs(target, 0, [])
return res

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

def dfs(num, i, path):
    if num==0:
        res.append(path)
        return
    for j in range(i, len(candidates)):
        if j>i and candidates[j-1]==candidates[j]:
            continue
        n = candidates[j]
        if num-n<0: continue
        dfs(num-n, j+1, path+[n])

candidates.sort()
res = []
dfs(target, 0, [])
return res

Previous二分搜索 Next遍历：BFS

Last updated 3 years ago

Was this helpful?